数学知识:相似三角形知识点有哪些
最近越来越多的小伙伴对于相似三角形知识点有哪些这方面的问题开始感兴趣,因为大家现在都是想要了解到此类的信息,那么既然现在大家都想要知道相似三角形知识点有哪些,小编今天就来给大家针对这样的问题做个科普介绍吧。
相似三角形非常重要,是初三几何知识中的核心,容易出现在压轴题,以下内容是小编整理的相似三角形的判定方法及相似三角形的常见模型,同学们要深刻体会,同时要结合专题进行练习。

(1)定义法:对应角相等,对应边成比例的两个三角形相似。
(2)平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角形与原三角形相似。
(3)判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两个三角形相似。简述为:两角对应相等,两三角形相似。
(4)判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹角相等,那么这两个三角形相似。简述为:两边对应成比例且夹角相等,两三角形相似。
(5)判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似。简述为:三边对应成比例,两三角形相似。
(6)判定直角三角形相似的方法:
①以上各种判定均适用
②如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似
③直角三角形被斜边上的高分成的两个直角三角形与原三角形相似
直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项
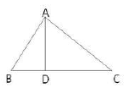
每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。如图,Rt△ABC中,∠BAC=90°,AD是斜边BC上的高,则有射影定理如下:
(1)(AD)2=BD·DC
(2)(AB)2=BD·BC
(3)(AC)2=CD·BC
注:由上述射影定理还可以证明勾股定理。即(AB)2+(AC)2=(BC)2。
(1)A字型(正A,反A,A字形线簇模型)
(2)8字型(正8,反8,8字型线簇模型)
(3)一线三垂直
(4)一线三等角
(5)射影定理
(6)三角形内接矩形
(7)三平行模型
相似三角形的性质定理:(1)相似三角形的对应角相等.
(2)相似三角形的对应边成比例.
(3)相似三角形的对应高线的比,对应中线的比和对应角平分线的比都等于相似比.
(4)相似三角形的周长比等于相似比.
(5)相似三角形的面积比等于相似比的平方.
相似三角形的传递性
如果△ABC∽△A1B1C1,△A1B1C1∽△A2B2C2,那么△ABC∽A2B2C2
